FFT 알고리즘
FFT Algorithm (Fast Fourier Transform Algorithm)
-
FFT(Fast Fourier Transform) 알고리즘은DFT(Discrete Fourier Transform)에서 파생되어 왔다. 결론부터 말하자면DFT에서 시간적 효율성을 가져온 알고리즘이라 볼 수 있겠다. -
FFT는DFT(Discrete Fourier Transform),IDFT(Inverse Discrete Fourier Transform) 모두 가능하며대표적인
FFT알고리즘 으로는쿨리-튜키(Cooley-Tukey)알고리즘이 있다. 이는Butterfly Algorithm이라고도 불린다. 그 이유는 포스트 하단부에서 확인하도록 할 것이다.
DFT와 비교했을 때에 왜, 얼마나 효율적일까?
DFT (Discrete Fourier Transform)
DFT를 설명하기에 앞서,Sampling을 하는 이유에 대해 살짝 짚고 넘어가야 한다.DFT에Sampling한 개수가 변수로 들어가 있기 때문이다.
Digital System은 이산화 되어있는데 , 이를 표현하기 위해서는 Series를 Discrete 하게 바꿔 줄 필요가 있다. 때문에 연속적인 값인 주파수를 일정 크기로 나누어Sampling을 해야 한다.
위 수식을 보면 주파수 f는 연속적인 값을 가지고 있다.
이 연속적인 값을 이산적으로 바꿔주기위해 Sampling을 하면,
이처럼 된다.
이는 주파수 f를 N개 Sampling 혹은 N만큼의 길이로 나누었다고 볼 수 있다. ( n은 정수이므로 이산적으로 표현)
FFT (Fast Fourier Transform)
FFT는 기본적으로Divide and Conquer기법에 착안하여 나온 알고리즘이다.
- 이처럼 N개의
Sampling값을 N/2개로 나누어 연산후 다시 결합하는 형식으로 N=2가 될때 까지 이 작업을 반복한다.
- N=8 -> 2개의 N=4 로 나누어 연산 후 결합
- N=4 -> 2개의 N=2 로 나누어 연산 후 결합
결론
- 기본적으로
DFT연산을 유지하고 있으나 , 이를짝수개로Divide and Conquer함으로써연산량 줄이기로 인해시간적 효율을 가져오게 된다.
때문에 2^m개 일때 연산가능하다는 조건이 붙는다.
만약 2^m개가 아니라면 , 부족한 개수만큼 0값을 추가하여 2^m개로 맞추어 준 뒤, 실존하는 값들을 확장 시킨다.
DFT와FFT연산량 차이 이다. 저번에 포스팅했던분할정복과 유사하게 곱셈량을 줄임으로써 계산 시간을 대폭 줄여 시간적 효율을 가져간 케이스 인 듯 하다. N이 증가 할수록 그 연산량은 큰 차이가 난다.
출처 사진 자료: 한성대학교 ppt (고속 푸리에 변환)
FFT Code
전체코드 ( 출처 : Columbia University FFT class)
Main Page Packages Class Hierarchy Compound List File List Compound Members
FFT.java
00001 /*
00002 * Copyright 2006-2007 Columbia University.
00003 *
00004 * This file is part of MEAPsoft.
00005 *
00006 * MEAPsoft is free software; you can redistribute it and/or modify
00007 * it under the terms of the GNU General Public License version 2 as
00008 * published by the Free Software Foundation.
00009 *
00010 * MEAPsoft is distributed in the hope that it will be useful, but
00011 * WITHOUT ANY WARRANTY; without even the implied warranty of
00012 * MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU
00013 * General Public License for more details.
00014 *
00015 * You should have received a copy of the GNU General Public License
00016 * along with MEAPsoft; if not, write to the Free Software
00017 * Foundation, Inc., 51 Franklin St, Fifth Floor, Boston, MA
00018 * 02110-1301 USA
00019 *
00020 * See the file "COPYING" for the text of the license.
00021 */
00022
00023 package com.meapsoft;
00024
00025
00033 public class FFT {
00034
00035 int n, m;
00036
00037 // Lookup tables. Only need to recompute when size of FFT changes.
00038 double[] cos;
00039 double[] sin; // cos,sin 배열 생성
00040
00041 double[] window;
00042
00043 public FFT(int n) {
00044 this.n = n;
00045 this.m = (int)(Math.log(n) / Math.log(2)); //2의 n승꼴로 표현하기위함
00046
00047 // Make sure n is a power of 2
00048 if(n != (1<<m))
00049 throw new RuntimeException("FFT length must be power of 2");
// m이 2의 n승 꼴이 아닐시 예외처리
00050
00051 // precompute tables
00052 cos = new double[n/2];
00053 sin = new double[n/2]; // 이부분이 divide and conquer을 실행하기위한 부분인듯하다.
00054
00055 // for(int i=0; i<n/4; i++) {
00056 // cos[i] = Math.cos(-2*Math.PI*i/n);
00057 // sin[n/4-i] = cos[i];
00058 // cos[n/2-i] = -cos[i];
00059 // sin[n/4+i] = cos[i];
00060 // cos[n/2+i] = -cos[i];
00061 // sin[n*3/4-i] = -cos[i];
00062 // cos[n-i] = cos[i];
00063 // sin[n*3/4+i] = -cos[i];
00064 // }
00065
00066 for(int i=0; i<n/2; i++) {
00067 cos[i] = Math.cos(-2*Math.PI*i/n);
00068 sin[i] = Math.sin(-2*Math.PI*i/n);
00069 }
00070 // summation
00071 makeWindow();
00072 }
00073
00074 protected void makeWindow() {
00075 // Make a blackman window:
00076 // w(n)=0.42-0.5cos{(2*PI*n)/(N-1)}+0.08cos{(4*PI*n)/(N-1)};
00077 window = new double[n];
00078 for(int i = 0; i < window.length; i++)
00079 window[i] = 0.42 - 0.5 * Math.cos(2*Math.PI*i/(n-1))
00080 + 0.08 * Math.cos(4*Math.PI*i/(n-1));
00081 }
00082 //MATLAB의 Blackman window 기능을 만드는 코드이다 중앙선을 기준으로 대칭인 그래프 생성
00083 public double[] getWindow() {
00084 return window;
00085 }
00086
00087
00088 /***************************************************************
00089 * fft.c
00090 * Douglas L. Jones
00091 * University of Illinois at Urbana-Champaign
00092 * January 19, 1992
00093 * http://cnx.rice.edu/content/m12016/latest/
00094 *
00095 * fft: in-place radix-2 DIT DFT of a complex input
00096 *
00097 * input:
00098 * n: length of FFT: must be a power of two
00099 * m: n = 2**m
00100 * input/output
00101 * x: double array of length n with real part of data
00102 * y: double array of length n with imag part of data
00103 *
00104 * Permission to copy and use this program is granted
00105 * as long as this header is included.
00106 ****************************************************************/
00107 public void fft(double[] x, double[] y)
00108 {
00109 int i,j,k,n1,n2,a;
00110 double c,s,e,t1,t2;
00111
00112
00113 // Bit-reverse
00114 j = 0;
00115 n2 = n/2;
00116 for (i=1; i < n - 1; i++) {
00117 n1 = n2;
00118 while ( j >= n1 ) {
00119 j = j - n1;
00120 n1 = n1/2;
00121 }
00122 j = j + n1;
00123
00124 if (i < j) {
00125 t1 = x[i];
00126 x[i] = x[j];
00127 x[j] = t1;
00128 t1 = y[i];
00129 y[i] = y[j];
00130 y[j] = t1;
00131 }
00132 } // Bit reverse는 재귀문을 for문으로 바꾸는 과정에, input -output의 n값이 대칭적으로
00133 //전환이 되므로 입력해주어야 한다. 자세한건 아래에서 다시보겠다.
00134 // FFT
00135 n1 = 0;
00136 n2 = 1;
00137
00138 for (i=0; i < m; i++) {
00139 n1 = n2;
00140 n2 = n2 + n2;
00141 a = 0;
00142
00143 for (j=0; j < n1; j++) {
00144 c = cos[a];
00145 s = sin[a];
00146 a += 1 << (m-i-1);
00147 // 하단의 for문이 주된 FFT연산기능을 하는 부분이다. 자세한 내용은 코드밖에서 보겠다.
00148 for (k=j; k < n; k=k+n2) {
00149 t1 = c*x[k+n1] - s*y[k+n1];
00150 t2 = s*x[k+n1] + c*y[k+n1];
00151 x[k+n1] = x[k] - t1;
00152 y[k+n1] = y[k] - t2;
00153 x[k] = x[k] + t1;
00154 y[k] = y[k] + t2;
00155 }
00156 }
00157 }
00158 }
00159
00160
00161
00162
00163 // Test the FFT to make sure it's working
00164 public static void main(String[] args) {
00165 int N = 8;
00166
00167 FFT fft = new FFT(N);
00168
00169 double[] window = fft.getWindow();
00170 double[] re = new double[N];
00171 double[] im = new double[N];
00172
00173 // Impulse
00174 re[0] = 1; im[0] = 0;
00175 for(int i=1; i<N; i++)
00176 re[i] = im[i] = 0;
00177 beforeAfter(fft, re, im);
00178
00179 // Nyquist
00180 for(int i=0; i<N; i++) {
00181 re[i] = Math.pow(-1, i);
00182 im[i] = 0;
00183 }
00184 beforeAfter(fft, re, im);
00185
00186 // Single sin
00187 for(int i=0; i<N; i++) {
00188 re[i] = Math.cos(2*Math.PI*i / N);
00189 im[i] = 0;
00190 }
00191 beforeAfter(fft, re, im);
00192
00193 // Ramp
00194 for(int i=0; i<N; i++) {
00195 re[i] = i;
00196 im[i] = 0;
00197 }
00198 beforeAfter(fft, re, im);
00199
00200 long time = System.currentTimeMillis();
00201 double iter = 30000;
00202 for(int i=0; i<iter; i++)
00203 fft.fft(re,im);
00204 time = System.currentTimeMillis() - time;
00205 System.out.println("Averaged " + (time/iter) + "ms per iteration");
00206 }
00207
00208 protected static void beforeAfter(FFT fft, double[] re, double[] im) {
00209 System.out.println("Before: ");
00210 printReIm(re, im);
00211 fft.fft(re, im);
00212 System.out.println("After: ");
00213 printReIm(re, im);
00214 }
00215
00216 protected static void printReIm(double[] re, double[] im) {
00217 System.out.print("Re: [");
00218 for(int i=0; i<re.length; i++)
00219 System.out.print(((int)(re[i]*1000)/1000.0) + " ");
00220
00221 System.out.print("]\nIm: [");
00222 for(int i=0; i<im.length; i++)
00223 System.out.print(((int(im[i]*1000)/1000.0) + " ");
00224
00225 System.out.println("]");
00226 }
00227 }
Generated on Tue Feb 6 19:02:26 2007 for MEAPsoft by doxygen1.2.18
Main code
for (k=j; k < n; k=k+n2) {
00149 t1 = c*x[k+n1] - s*y[k+n1]; // x[k+n1]*exp[-i*pi*2/n]와 같이 볼 수 있다.
00150 t2 = s*x[k+n1] + c*y[k+n1];
00151 x[k+n1] = x[k] - t1;
00152 y[k+n1] = y[k] - t2;
00153 x[k] = x[k] + t1;
00154 y[k] = y[k] + t2;
00155 }
이 코드를 살펴보기 위해서는 FFT Algorithm이 어떤식으로 세워졌는지 알아야한다.
- Divide and Conquer 개념을 기반으로 홀 , 짝으로 구분한다.
그럼 위와같은 식을 얻을 수 있는데, 결과적으로 이와 같은 식을 얻을 수 있다. (4)번과 같은 식을 구현한것이 위에 있는 코드이다.
비트반전
- 비트반전은 왜 필요할까?

- 왼쪽은 N=8을 한번에 계산한 것이고, 오른쪽은 N/2하여 계산 하며 합치는 과정이다.
- 이처럼 기존 N에서 절반씩 계산하여 합치도록 코드를 짜게 되면 재귀구문으로 돌리게 되는데, 재귀구문은 코드는 쉬울 수 있으나시간적으로 효율적이지 않다. 때문에 for문으로 고쳐주어야 할 필요성이 있는데 이를 위해 비트 반전이 필요하다.

-
N=8을 계산하기 위해 , 최소 수인 N=2 부터 계산해온 계산이다. 계산을 도식화 하기위해 그린 화살표가 나비모양과 비슷하다고 하여
Butterfly Algoritm이라고도 불리는 것이다. -
a(k)와 수평적으로 대응되는 A(k) 값을 살펴보면 두 k값이 서로 대칭되는 값임을 알 수 있다.
떄문에 A(k)를 계산하기 위해서 bit-reverse 가 필요하다.
비트반전 사진출처https://casterian.net/archives/297
Nyquist
-
프로세서의 측정속도에 비해 주파수가 너무 빠른 신호는 측정할 수 없음.
- 즉 , sampling period 의 절반이상 주파수는 측정 할 수 없음을 말함.
EX)
Samplign period = 0.1sec
측정 가능 주파수 = 10Hz // 즉 Nyquist frequency = 5Hz 이므로 그 아래는 측정가능하나 그 이후는 어려움
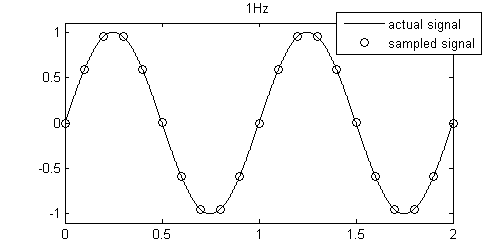
- 이처럼 1Hz 는 무난하게 그 주파수를 측정할 수 있다.
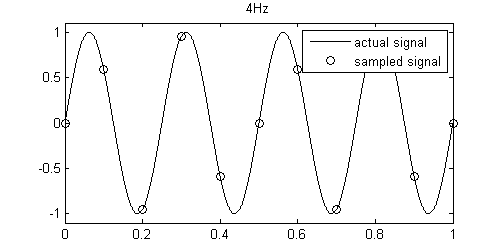
- 측정은 가능하나 상대적으로 측정이 더 어려워 졌음을 볼 수 있다.

- sampled된 signal이 다 같은 위치에 있는 것을 볼 수 있다. 이는 측정이 되지 않았다고 생각할 수 있다.
이제 Nyquist frequency 를 넘어서는 값들을 살펴보겠다.
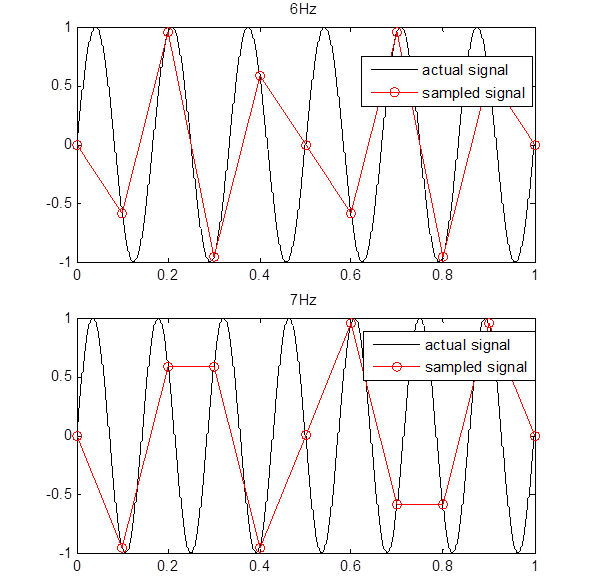
- 이처럼 sampled signal 이 기존의 파형을 나타내기 어려움을 볼 수 있다.
Nyquist출처http://blog.naver.com/PostView.nhn?blogId=lagrange0115&logNo=220621104750
결과값 관찰하기
Problem)
-
x(t) = 3cos(20πt) + 6sin(30πt - 3/(4π)), 0 <= t <= 1 -> 주파수 변환한 X(f)의 그래프 그리기
-
우리에겐 MATLAB이라는 좋은 Tool이 있으므로 이미 구현되어있는
fft를 사용해 보았다.
MATLAB / 전체코드
fs = 1000
t =0:1/fs:1
x = 3*cos(20*pi*t)+6*sin(30*pi*t-3/(4*pi))
X = fft(x)
N = length(x)
n =0:N-1
f = fs*n/N
plot(f,2*abs(X)/N)
- 결과값이 나오긴 했지만 도저히 어떤값인지 가시적으로 잘 보이지 않는다.
수정
fs = 1000
t =0:1/fs:1
x = 3*cos(20*pi*t)+6*sin(30*pi*t-3/(4*pi))
X = fft(x)
N = length(x)
n =0:N-1
f = fs*n/N
cutoff = ceil(N/2)
cutoff =50
X = X(1:cutoff)
f = f(1:cutoff)
plot(f,2*abs(X)/N)

- 상당히 만족스러운 결과값을 얻을 수 있었다.
X = 10Hz , 15Hz ;
Plot 전처리 해석
cutoff = ceil(N/2) // 굳이 음의 주파수를 확인할 필요없으므로
cutoff =50 // 위에서 반토막 내주었으나 우리가 관찰하려는 주파수가 너무 작은수여서 잘 보이지 않았다. 때문에 시각적인 확보를 위해 인위적으로 50까지만 보겠다고 추가 설정 해주었다.
X = X(1:cutoff) // 관찰하려는 그래프 y축설정
f = f(1:cutoff) // 관찰하려는 그래프 x축설정
plot(f,2*abs(X)/N) // y축값에서 2배를 해주는 이유는 양의주파수+음의주파수 값이 결과값이므로 값이 반으로 나뉘어 양쪽으로 나오게 된다. 우리는 굳이 두쪽을 다 확인할 필요가 없으므로 한쪽만 보고 power을 판단하기 위하여 2배를 해주는 것이다.
결과
fs = 1000
t =0:1/fs:1
x = 3*cos(20*pi*t)+6*sin(30*pi*t-3/(4*pi))
X = fft(x)
N = length(x)
n =0:N-1
f = fs*n/N
cutoff =ceil(N/2)
cutoff =100
x = x(1:cutoff)
X = X(1:cutoff)
f = f(1:cutoff)
plot(f,abs(x),'--r')
hold on
plot(f,2*abs(X)/N,'--g')
- 가존그래프와 비교 결과
Leave a comment